
The computation of any static "offset" is based on the assumption that (according to the Langmuir evaporation law) the observed ratio robs of an evaporated sample should always be larger
(by the factor of ) as the ratio RS in the bulk of the sample at a given time (or smaller, if the ratios are defined as "heavy-to-light").
(by the factor of ) as the ratio RS in the bulk of the sample at a given time (or smaller, if the ratios are defined as "heavy-to-light").

And, correspondingly, we obtain, using the CalTech standard value:
In particular :The ratio in the bulk at the beginning of the evaporation is the "true" ratio RT= RS(t=0)
If this is not the case, one may, amongst other explanations, explain such a discrepancy by the existance of cut-off effects for the ion beam in its way through the ion optical system.
In fact, the data of files F4 and F12 were (probably) taken with a small magnet in the ion source (to deflect electrons which may destroy the entrance slit in negative ion operation), but which is not needed for positive ions. Data of file P12 are definitely taken after the removal of such a deflection magnet. In fact,the observed "offset" of P12 data is significantly smaller.
One may try to correct the observed ratios for such an offset by a recalculation of these ratios, using the offset as measured at the beginning of the data acquisition. Such a re-calculation would lead to ratios (rcorr) as they would be observed in the vapor phase just on top of the evaporation filament:
If this is not the case, one may, amongst other explanations, explain such a discrepancy by the existance of cut-off effects for the ion beam in its way through the ion optical system.
In fact, the data of files F4 and F12 were (probably) taken with a small magnet in the ion source (to deflect electrons which may destroy the entrance slit in negative ion operation), but which is not needed for positive ions. Data of file P12 are definitely taken after the removal of such a deflection magnet. In fact,the observed "offset" of P12 data is significantly smaller.
One may try to correct the observed ratios for such an offset by a recalculation of these ratios, using the offset as measured at the beginning of the data acquisition. Such a re-calculation would lead to ratios (rcorr) as they would be observed in the vapor phase just on top of the evaporation filament:
And the (much smaller) static offsets, assuming this "New Standard" would be :
r1(142/144) and r3(146/148) are normalized, using rN(144/146) as the "normalizing" ratio.
All ratios are defined (unidirectionally) as "light over heavy". This kind of definition is arbitrary, but it enables us to also evaluate the data using the so called "explicite" Rayleigh law, if needed.
The "true" value for 144/146Nd was assumed to be RN = 1.38523 ("La Jolla").
The evaluation of all 3 files show excellent internal precision (sn-1 < 40 ppm for F4 resp. F12, and <15 ppm for P12). The calculated residual fractionation after the correction (Expo law) is practically negligible. It is in the order of 2 ppm/h, i.e., it is far within measuring precision.
However :The fractionation corrected run means (R1 resp. R3) are by no means identical for static discrimination corrected or straight raw data, respectively.
We obtain, using the LaJolla standard value:
All ratios are defined (unidirectionally) as "light over heavy". This kind of definition is arbitrary, but it enables us to also evaluate the data using the so called "explicite" Rayleigh law, if needed.
The "true" value for 144/146Nd was assumed to be RN = 1.38523 ("La Jolla").
The evaluation of all 3 files show excellent internal precision (sn-1 < 40 ppm for F4 resp. F12, and <15 ppm for P12). The calculated residual fractionation after the correction (Expo law) is practically negligible. It is in the order of 2 ppm/h, i.e., it is far within measuring precision.
However :The fractionation corrected run means (R1 resp. R3) are by no means identical for static discrimination corrected or straight raw data, respectively.
We obtain, using the LaJolla standard value:
RN(F4) and RN(F12), which originate from runs, taken with similar instrumental conditions
(additional magnet), are equal within measuring precision. These values are relatively near to the
"CalTech" value, but significantly away from "La Jolla".
The normalized, i.e. the "true" ratios using the "New Standard" (the average of all three files) are,
thus,
The normalized, i.e. the "true" values are still different for corrected and not corrected raw data, but much less ( ~ 20 ppm resp. ~50 ppm).
And still, we find : Ro1 > Rcorr1 whereas Ro3 < Rcorr3.
This finding suggests to search for an RN value, for which the corrected and not corrected normalized R1- or R3-ratios possibly become equal, respectively.
Hence, RN has been systematically varried in the range [1.366< RN <1.382], and plotted against the differences of the means of the corrected and not corrected normalized data.
In fact, R1 gets continuously smaller with growing RN, whereas R3 continuously grows, and the differences get zero at values RN - values, which are very near to each other, but they slightly depend on the raw data itself. One gets:
And still, we find : Ro1 > Rcorr1 whereas Ro3 < Rcorr3.
This finding suggests to search for an RN value, for which the corrected and not corrected normalized R1- or R3-ratios possibly become equal, respectively.
Hence, RN has been systematically varried in the range [1.366< RN <1.382], and plotted against the differences of the means of the corrected and not corrected normalized data.
In fact, R1 gets continuously smaller with growing RN, whereas R3 continuously grows, and the differences get zero at values RN - values, which are very near to each other, but they slightly depend on the raw data itself. One gets:
D) Discussion
If fractionation biases are produced by prefered evaporation of the lighter species of an isotope ratio, then the observed isotope ratio (light/heavy) is at any time larger than the isotope ratio in the bulk of the sample by a factor of (m1>m2). If this is not the case, static offsets, caused, e.g., by cutoff effects, may be the explanation.
If the size of such static offsets can be measured, one is able to "reconstruct" the non biased, plain evaporation induced ratio, which may then be used for calculating the fractionation corrected, i.e., the "true" isotope ratio by applying, for instance, the "Exponential Law" (Internal normalization).
In normal practice, static offsets are not seperately handled, before internal normalization is performed. In other words, one silently assumes that there are no static offsets or one hopes, that any possibly existing static offsets are "automatically" handled by the Expo Law, as if they were a kind of evaporation induced fractionation offsets.
If such an assumption would be correct, one would,thus, expect that reconstructed data (freed from static offsets) or plain raw data, respectively, would result in the same normalized, "true" isotope ratio.
Or, still another approach: One would apply "second order corrections".
Using data which are known to be statically biased one can show that the above assumption is wrong. In other words:
There are founded reasons that the result of an internal normalization not only depends on the knowledge of the "true" (or agreed upon) value of the normalizing ratio, but also on certain instrumental conditions like static biases. Hence, such normalized results are not comparable from instrument to instrument (laboratory to laboratory), as long as there is any uncertainty on the existance of static biases.
The weak point of this argumentation is the difficulty to measure the static offset with sufficient accuracy. This may have, at least, the following reasons:
(a) All available raw data are already fractionated by evaporation (because data are not acquired from the very beginning of the heating of the sample), or data may be "falsified" by other effects, like the evaporation of molecular species with higher masses and, consequently, less fractionation bias.
(b) The assumed standard ratio does not reflect the true ratio of the normalizing ratio of the sample.
(c) One of the Faraday cups may show a cup offset (and should, therefore, be replaced).
In any case we have learnt: Internal normalization of high precision data does not necessarily mean highly accurate results. They, possibly, cannot be reproduced by another laboratory with a differently configured mass spectrometer.
If fractionation biases are produced by prefered evaporation of the lighter species of an isotope ratio, then the observed isotope ratio (light/heavy) is at any time larger than the isotope ratio in the bulk of the sample by a factor of (m1>m2). If this is not the case, static offsets, caused, e.g., by cutoff effects, may be the explanation.
If the size of such static offsets can be measured, one is able to "reconstruct" the non biased, plain evaporation induced ratio, which may then be used for calculating the fractionation corrected, i.e., the "true" isotope ratio by applying, for instance, the "Exponential Law" (Internal normalization).
In normal practice, static offsets are not seperately handled, before internal normalization is performed. In other words, one silently assumes that there are no static offsets or one hopes, that any possibly existing static offsets are "automatically" handled by the Expo Law, as if they were a kind of evaporation induced fractionation offsets.
If such an assumption would be correct, one would,thus, expect that reconstructed data (freed from static offsets) or plain raw data, respectively, would result in the same normalized, "true" isotope ratio.
Or, still another approach: One would apply "second order corrections".
Using data which are known to be statically biased one can show that the above assumption is wrong. In other words:
There are founded reasons that the result of an internal normalization not only depends on the knowledge of the "true" (or agreed upon) value of the normalizing ratio, but also on certain instrumental conditions like static biases. Hence, such normalized results are not comparable from instrument to instrument (laboratory to laboratory), as long as there is any uncertainty on the existance of static biases.
The weak point of this argumentation is the difficulty to measure the static offset with sufficient accuracy. This may have, at least, the following reasons:
(a) All available raw data are already fractionated by evaporation (because data are not acquired from the very beginning of the heating of the sample), or data may be "falsified" by other effects, like the evaporation of molecular species with higher masses and, consequently, less fractionation bias.
(b) The assumed standard ratio does not reflect the true ratio of the normalizing ratio of the sample.
(c) One of the Faraday cups may show a cup offset (and should, therefore, be replaced).
In any case we have learnt: Internal normalization of high precision data does not necessarily mean highly accurate results. They, possibly, cannot be reproduced by another laboratory with a differently configured mass spectrometer.
(1)
(2)
(3)
No further assumptions are made, especially nothing on the numeric value of parameter P. The simple physical message of the Expo law is, thus, the assuption of the ruling role of the mass ratio.
For fractionation processes which are only determined by a thermal evaporation process, one may assume P = ½ for the beginning of the evaporation. E.g.:
For fractionation processes which are only determined by a thermal evaporation process, one may assume P = ½ for the beginning of the evaporation. E.g.:
(4)
q(t) describes the (oftenly complicated) time dependence of the raw fractionation profile. One
would, e.g., expect:
(5)
Parameter s must, as well, not be time dependent, to reflect the intentions of the Expo Law. Please note: Faraday cup effects are not covered with this equation.
If we have an isotopic system with at least 3 isotopic species, we can calculate two non trivial isotope ratios (robs1 and robs2), and, for both ratios the above equ. (5) is valid.
If, additionally, the "true" ratio (RT2) of one of these ratios is known, we can compute the "true" ratio (RT1) of the other ratio just by eliminating parameter P(t), which is identical for all simultaniously evaporating isotopic species of the same isotopic system. The normalizing formula would thus be as follows:
If we have an isotopic system with at least 3 isotopic species, we can calculate two non trivial isotope ratios (robs1 and robs2), and, for both ratios the above equ. (5) is valid.
If, additionally, the "true" ratio (RT2) of one of these ratios is known, we can compute the "true" ratio (RT1) of the other ratio just by eliminating parameter P(t), which is identical for all simultaniously evaporating isotopic species of the same isotopic system. The normalizing formula would thus be as follows:
(6)
In summary: As long as static and dynamic mass discriminations only depend on the mass ratio of the isotopic species, then the Expo law makes no difference, i.e., static and dynamic discriminations are both eliminated in the same way by the normalization formula.
Especially, we may thus expect that uncorrected raw ratios on the one side, and corrected ratios (equ. 2) on the other side, may lead to the very same result.
C) Evaluation
Three raw data files (F4, F12, P12) have been used to test the above statements. A special, symmetric evaluation scheme is choosen, in order to exclude other possibly mass-dependent effects, for instance, to exclude influences from a mass dependent parameter s :
Especially, we may thus expect that uncorrected raw ratios on the one side, and corrected ratios (equ. 2) on the other side, may lead to the very same result.
C) Evaluation
Three raw data files (F4, F12, P12) have been used to test the above statements. A special, symmetric evaluation scheme is choosen, in order to exclude other possibly mass-dependent effects, for instance, to exclude influences from a mass dependent parameter s :
| 142 | 144 | 146 | 148 | |||
| I | <------ r1 ------> | I | <------ rN ------> | I | <------ r3 ------> | I |
The normalized, i.e. the so called "true" values are significantly different (~ 100 ppm) for corrected (Rcorr) and not corrected (Ro) raw data.
Moreover, we find : Ro1 > Rcorr1 whereas Ro3 < Rcorr3,
i.e.: The values are, so to speak, "mirrored" at the normalizing ratio.
If the also supposedly "known" CalTech standard ratio (RN = 1.38103) is used instead, then the observed static discriminations, consequently, are smaller:
Moreover, we find : Ro1 > Rcorr1 whereas Ro3 < Rcorr3,
i.e.: The values are, so to speak, "mirrored" at the normalizing ratio.
If the also supposedly "known" CalTech standard ratio (RN = 1.38103) is used instead, then the observed static discriminations, consequently, are smaller:
Diese Seite steht auch als PDF-Datei zum Download bereit - bitte klicken Sie auf das PDF-Logo links.

A) Observations
I have analyzed the raw data of three TRITON generated data files of approx. The same lenght (~ 11.5 h) of an Ames Nd standard sample. Data acquisition parameters are said to be identical.
Files :
F4 and F12 obtained from J. Schwieters,
P12 obtained from G. Caro.
Using the La Jolla standard value (RN = R144/146 = 1.3852), one observes a remarkable static offset of the observed raw ratio r144/146 :
I have analyzed the raw data of three TRITON generated data files of approx. The same lenght (~ 11.5 h) of an Ames Nd standard sample. Data acquisition parameters are said to be identical.
Files :
F4 and F12 obtained from J. Schwieters,
P12 obtained from G. Caro.
Using the La Jolla standard value (RN = R144/146 = 1.3852), one observes a remarkable static offset of the observed raw ratio r144/146 :
r N(0) is the raw ratio of the i144 and i146 ion currents at the very beginning of the data acquisition. The question is:
Has this offset any influence on the fractionation corrected 'true' ratio ?
B) Theory
Has this offset any influence on the fractionation corrected 'true' ratio ?
B) Theory
Other, not time dependent (i.e. "static") mass discriminations may be described by an additional
parameter s. If one may assume, that also such discriminations are physically determined by the
mass ratio only (e.g., magnetic deflections), one would, e.g., write:
F4:
F12:
P12:
F12:
P12:
3.917 o/oo
3.852 o/oo
2.477 o/oo
3.852 o/oo
2.477 o/oo
}
}
}
}
}
per mass unit
F4:
F12:
P12:
F12:
P12:
- 0.012 o/oo
- 0.023 o/oo
- 0.032 o/oo
- 0.023 o/oo
- 0.032 o/oo
}
}
}
}
}
per mass unit
F4:
F12:
P12:
Average:
F12:
P12:
Average:
R1
1.1342 94
1.1342 90
1.1342 94
1.1342 93
1.1342 94
1.1342 90
1.1342 94
1.1342 93
F4:
F12:
P12:
Average:
F12:
P12:
Average:
Not corrected data:
Corrected data:
R3
2.9690 00
2.9690 99
2.9690 34
2.9690 11
2.9690 00
2.9690 99
2.9690 34
2.9690 11
1.1342 74
1.1342 82
1.1342 49
1.1342 92
1.1342 82
1.1342 49
1.1342 92
2.96 9050
2.96 9018
2.96 8897
2.96 9013
2.96 9018
2.96 8897
2.96 9013
From F4:
From F12:
From P12:
Average:
From F12:
From P12:
Average:
RN
RN
RN
RN
RN
RN
RN
= 1.3745
= 1.3755
= 1.3785
= 1.3762
= 1.3755
= 1.3785
= 1.3762
R1
1.1383 27
1.1383 22
1.1382 26
1.1382 92
1.1383 27
1.1383 22
1.1382 26
1.1382 92
F4:
F12:
P12:
Average:
F12:
P12:
Average:
F4:
F12:
P12:
Average:
F12:
P12:
Average:
Not corrected data:
Corrected data:
R3
2.9882 57
2.9882 21
2.9882 57
2.9882 45
2.9882 57
2.9882 21
2.9882 57
2.9882 45
1.1382 51
1.1382 59
1.1382 96
1.1382 69
1.1382 59
1.1382 96
1.1382 69
2.979 459
2.979 426
2.979 378
2.967 421
2.979 426
2.979 378
2.967 421
R1
1.1418 44
1.1418 40
1.1418 44
1.1418 43
1.1418 44
1.1418 40
1.1418 44
1.1418 43
F4:
F12:
P12:
Average:
F12:
P12:
Average:
F4:
F12:
P12:
Average:
F12:
P12:
Average:
Not corrected data:
Corrected data:
R3
2.9882 57
2.9882 21
2.9882 57
2.9882 45
2.9882 57
2.9882 21
2.9882 57
2.9882 45
1.1417 20
1.1417 28
1.1417 65
1.1417 37
1.1417 28
1.1417 65
1.1417 37
2.9885 39
2.9885 06
2.9885 58
2.9885 01
2.9885 06
2.9885 58
2.9885 01
F4:
F12:
P12:
F12:
P12:
2.386 o/oo
1.985 o/oo
0.951 o/oo
1.985 o/oo
0.951 o/oo
}
}
}
}
}
per mass unit
This static offest is defined as
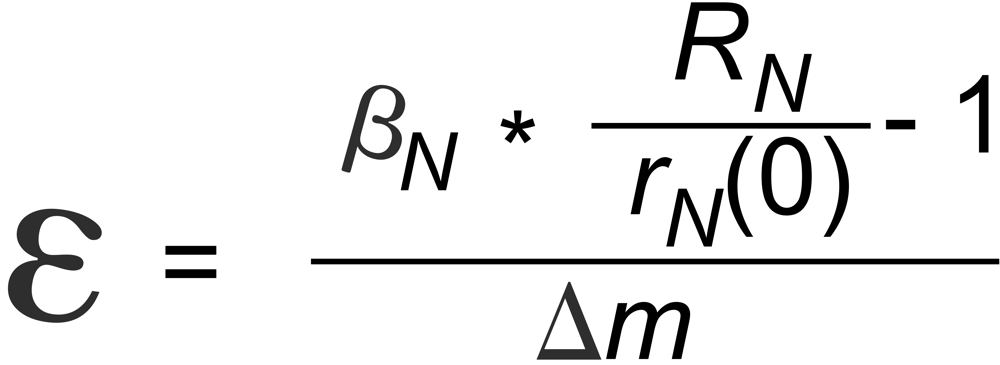


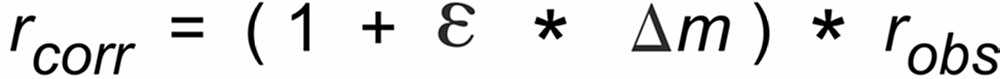
These "corrected", static offset free ratios may then be used to be further corrected for evaporation induced fractionation, using, for instance, the common "Exponential Law" ("Expo law").
The Exponential Law makes a simple basic assumption: The differences between the true (RT) and the observed (robs) isotope ratios depend on the ratio of the masses (m1, m2) of the two isotopic species of the ion current ratio, and
on a time dependent parameter P. It describes the time dependence of the fractionation, and it is identical for all ratios of the given isotopic system at a given time . It must not depend on mass.
The Exponential Law makes a simple basic assumption: The differences between the true (RT) and the observed (robs) isotope ratios depend on the ratio of the masses (m1, m2) of the two isotopic species of the ion current ratio, and
on a time dependent parameter P. It describes the time dependence of the fractionation, and it is identical for all ratios of the given isotopic system at a given time . It must not depend on mass.
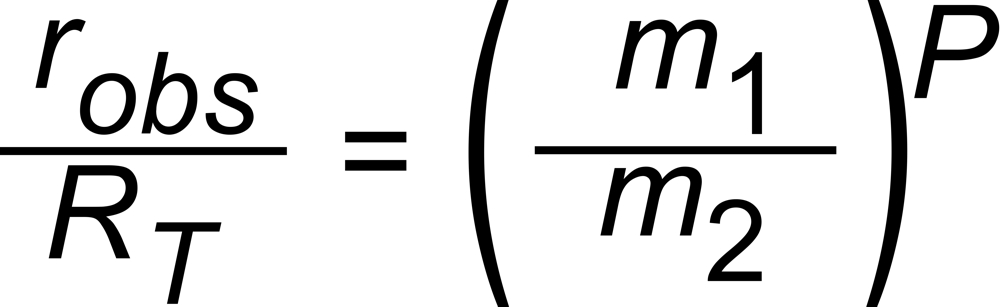
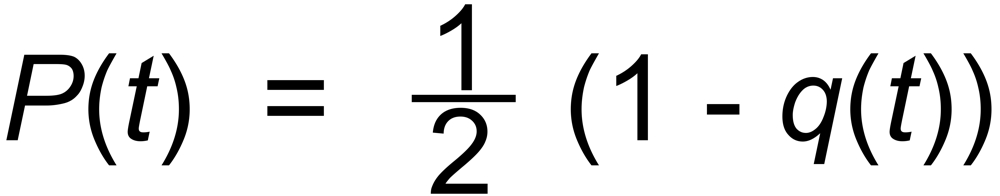
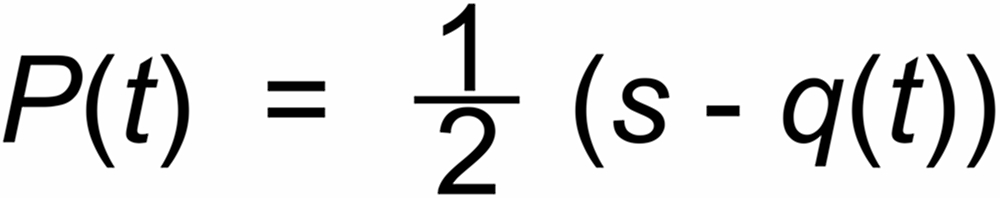
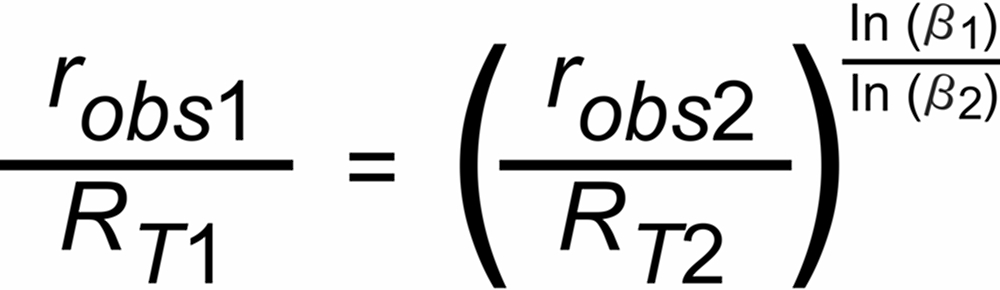

Dr. Karleugen Habfast: ToFC - "Seperate Correction" of static discriminations








